PEMDAS: The Mathematical Order of Operations
Introduction:
To evaluate a mathematical expression, we perform the various operations. However, we do not perform them in any random order. We use the order of operations. This is a sequence of rules for evaluating such expressions.
Learning:
Performing Calculations Using the Order of Operations
To evaluate a mathematical expression, we perform the various operations. However, we do not perform them in any random order. We use the order of operations. This is a sequence of rules for evaluating such expressions.
The order of operations is the order in which all algebraic expressions should be simplified. Often the meaning of a complex expression changes depending upon the order in which it is calculated. The order of operations is:
Parentheses means brackets ( )
Exponents (and Roots) means power
Multiplication & Division
Addition & Subtraction
This means that expressions within parentheses are evaluated first, then exponents (including roots, i.e. radicals), then multiplication and division (at the same level), and finally addition and subtraction (at the same level). If there are multiple operations at the same level on the order of operations, move from left to right.
There is a number of different abbreviations for memorizing the order. PEMDAS, BEDMAS and BODMAS (B is Brackets) are common. Another common way to remember the order is the mnemonic
“Please Excuse My Dear Aunt Sally”
with the beginning letters standing for each operation. Whichever mnemonic you use, be aware that multiplication does not always come before division, and addition does not always come before subtraction. For example:
If you have an expression like:
you work like this:
- First notice that, there are no Parentheses or Exponents
- Move to Multiplication and Division. There’s only the one multiplication,
3 × 3 – 5 + 2
so do that first and end up with 9 – 5 + 2.
- Now move to Addition and Subtraction, working left to right.
9 – 5 + 2 to get 4 + 2
- and finally the addition
4 + 2 to give 6.
If we had blindly done the addition (5 + 2) first, the answer would be 2, which is wrong!
Creating Complex Formulas (Controlling the Order of Operations)
Complex formulas can be created within a cell, but it is critical to remember the order of operations. This requires that the order of mathematical operations be controlled to get an accurate result. Excel will calculate the result of the formula according to the order of operations, and will move left to right in the formula.
Standard Order of Mathematical Operations
|
Order |
|
|
( ) |
Override Standard Order: Any mathematical computations placed in parentheses are performed first and override the standard order of operations. If there are layers of parentheses used in a formula, Excel computes the innermost parentheses first and the outermost parentheses last. |
|
^ |
First: Excel executes any exponential computations first. |
|
* or / |
Second: Excel performs any multiplication or division computations second. When there are multiple instances of these computations in a formula, they are executed in order from left to right. |
|
+ or − |
Third: Excel performs any addition or subtraction computations third. When there are multiple instances of these computations in a formula, they are executed in order from left to right. |
How would the following formulas be resolved?
Given the following Excel worksheet, with values in cells D1, B2, C2, A3, and C4, refer to the table below to see how the order of operations can be controlled in the example formula
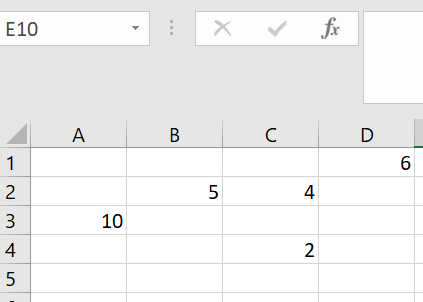
How would Excel calculate the formula =D1*C2+B2-A3^C4?
The order of operations would be:
- There are no parentheses ( ) – move to the next step
- There is an exponential, so calculate A3^C4 first
=D1*C2+B2- A3^C4
=D1*C2+B2 – 100
- Multiply or divide, left to right, D1*C2
= 6*4 + B2 – 100
= 24 + B2 – 100
- Addition or subtraction, left to right
= 24 + B2 – 100
= 24 + 5 – 100
= -71
The parentheses were added to this formula to control the order of operations. How would Excel now calculate the formula =D1*(C2+B2)-A3^C4 ?
The order of operations would be:
- There ARE parentheses ( ) so that would be evaluated first (C2+B2)
=D1*(C2+B2)-A3^C4
=D1*(4 + 5) – A3^C4
=D1* 9 – A3^C4
- There is an exponential, so calculate A3^C4
=D1* 9 – A3^C4
=D1* 9 – 100
- Multiply or divide, left to right, D1*9
=D1* 9 – 100
=6 * 9 -100
=54 – 100
- Addition or subtraction, left to right
= -46
As you can see, parentheses () make a huge difference in how Excel calculates the formula. It is important to plan your formula’s wisely in order to have your spreadsheet correctly calculate.
Summary:
Excel’s ability to complete complex mathematical calculations is what makes Excel very powerful. Excel calculations will always follow the mathematical order of operations, PEMDAS, when solving any formula or function. Parentheses must be used to control the order of operations when necessary for complex formulas. It is important to note that the accuracy of the output produced by a formula depends on how it is constructed. Therefore, always check the result of your formula to see whether it makes sense with data in your worksheet.
Sources:
College Algebra. Authored by: OpenStax College Algebra. Provided by: OpenStax. Located at: http://cnx.org/contents/9b08c294-057f-4201-9f48-5d6ad992740d@3.278:1/Preface. License: CC BY: Attribution