Correlational Research

Introduction

In contrast to descriptive research, which is designed primarily to provide static pictures, correlational research involves the measurement of two or more relevant variables and an assessment of the relationship between or among those variables. Correlational research is a type of nonexperimental research in which the researcher measures two variables and assesses the statistical relationship (i.e., the correlation) between them with little or no effort to control extraneous variables. There are essentially two reasons that researchers interested in statistical relationships between variables would choose to conduct a correlational study rather than an experiment. The first is that they do not believe that the statistical relationship is a causal one. For example, a researcher might evaluate the validity of a brief extraversion test by administering it to a large group of participants along with a longer extraversion test that has already been shown to be valid. This researcher might then check to see whether participants’ scores on the brief test are strongly correlated with their scores on the longer one. Neither test score is thought to cause the other, so there is no independent variable to manipulate. In fact, the terms independent variable and dependent variable do not apply to this kind of research. The other reason that researchers would choose to use a correlational study rather than an experiment is that the statistical relationship of interest is thought to be causal, but the researcher cannot manipulate the independent variable because it is impossible, impractical, or unethical.

“Correlational Research.” Retrieved from http://open.lib.umn.edu/psychologyresearchmethods/chapter/7-2-correlational-research/. Licensed under CC-BY-NC-SA.

Correlational Research

One way of organizing the data from a correlational study with two variables is to graph the values of each of the measured variables using a scatter plot. A scatter plot is a visual image of the relationship between two variables. A point is plotted for each individual at the intersection of his or her scores for the two variables. When the association between the variables on the scatter plot can be easily approximated with a straight line, the variables are said to have a linear relationship.

When the straight line indicates that individuals who have above-average values for one variable also tend to have above-average values for the other variable, the relationship is said to be positive linear. Examples of positive linear relationships include those between height and weight, between education and income, and between age and mathematical abilities in children. In each case, people who score higher on one of the variables also tend to score higher on the other variable. Negative linear relationships, in contrast, occur when above-average values for one variable tend to be associated with below-average values for the other variable. Examples of negative linear relationships include those between the weight of a car and its gas mileage and between practice on and errors made on a learning task. In these cases, people who score higher on one of the variables tend to score lower on the other variable.

Relationships between variables that cannot be described with a straight line are known as nonlinear relationships. In this case there is no relationship at all between the two variables, and they are said to be independent. For example, let’s look at the type of relationship that frequently occurs between anxiety and performance. Increases in anxiety from low to moderate levels are associated with performance increases, whereas increases in anxiety from moderate to high levels are associated with decreases in performance. Relationships that change in direction and thus are not described by a single straight line are called curvilinear relationships.

“English Schools Cross Country.” Retrieved from https://www.flickr.com/photos/adamkr/4448367111. Licensed under CC-BY-SA-2.0

The most common statistical measure of the strength of linear relationships among variables is the Pearson correlation coefficient, which is symbolized by the letter r. The value of the correlation coefficient ranges from r = –1.00 to r = +1.00. The direction of the linear relationship is indicated by the sign of the correlation coefficient. Positive values of r (such as r = .34 or r = .67) indicate that the relationship is positive linear (i.e., the pattern of the dots on the scatter plot runs from the lower left to the upper right), whereas negative values of r (such as r = –.30 or r = –.72) indicate negative linear relationships (i.e., the dots run from the upper left to the lower right). The strength of the linear relationship is indexed by the distance of the correlation coefficient from zero (its absolute value). For instance, r = –.54 is a stronger relationship than r = .30, and r = .72 is a stronger relationship than r = –.57. Because the Pearson correlation coefficient only measures linear relationships, variables that have curvilinear relationships are not well described by r, and the observed correlation will be close to zero.

It is also possible to study relationships among more than two measures at the same time. A research design in which more than one predictor variable is used to predict a single outcome variable is analyzed through multiple regression (Aiken & West, 1991). Multiple regression is a statistical technique, based on correlation coefficients among variables, that allows predicting a single outcome variable from more than one predictor variable.

This image shows a multiple regression analysis in which three predictor variables are used to predict a single outcome variable. The use of multiple regression analysis shows an important advantage of correlational research designs—they can be used to make predictions about a person’s likely score on an outcome variable (e.g., job performance) based on knowledge of other variables.

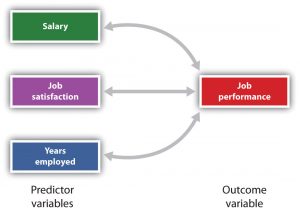
Stangor, C. (2017). Introduction to psychology. Boston, MA: Flatworld.
Aiken, L., & West, S. (1991). Multiple regression: Testing and interpreting interactions. Newbury Park, CA: Sage.
Stangor, C. (2017). Introduction to psychology. Boston, MA: Flatworld.

Interpreting Correlational Research

An important limitation of correlational research designs is that they cannot be used to draw conclusions about the causal relationships among the measured variables. Consider, for instance, a researcher who has hypothesized that viewing violent behavior will cause increased aggressive play in children. He has collected, from a sample of fourth-grade children, a measure of how many violent television shows each child views during the week, as well as a measure of how aggressively each child plays on the school playground. From his collected data, the researcher discovers a positive correlation between the two measured variables.

CCO

Although this positive correlation appears to support the researcher’s hypothesis, it cannot be taken to indicate that viewing violent television causes aggressive behavior. Although the researcher is tempted to assume that viewing violent television causes aggressive play, there are other possibilities.

Stangor, C. (2017). Introduction to psychology. Boston, MA: Flatworld.

One alternate possibility is that the causal direction is exactly opposite from what has been hypothesized. Perhaps children who have behaved aggressively at school develop residual excitement that leads them to want to watch violent television shows at home.

Stangor, C. (2017). Introduction to psychology. Boston, MA: Flatworld.

Still another possible explanation for the observed correlation is that it has been produced by the presence of a common-causal variable (also known as a third variable). A common-causal variable is a variable that is not part of the research hypothesis but that causes both the predictor and the outcome variable and thus produces the observed correlation between them. In our example a potential common-causal variable is the discipline style of the children’s parents. Parents who use a harsh and punitive discipline style may produce children who both like to watch violent television and who behave aggressively in comparison to children whose parents use less harsh discipline.

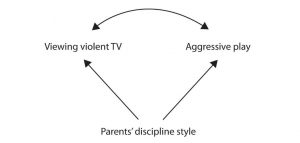
Stangor, C. (2017). Introduction to psychology. Boston, MA: Flatworld.

In this case, television viewing and aggressive play would be positively correlated (as indicated by the curved arrow between them), even though neither one caused the other but they were both caused by the discipline style of the parents (the straight arrows). When the predictor and outcome variables are both caused by a common-causal variable, the observed relationship between them is said to be spurious. A spurious relationship is a relationship between two variables in which a common-causal variable produces and “explains away” the relationship. If effects of the common-causal variable were taken away, or controlled for, the relationship between the predictor and outcome variables would disappear. The relationship between aggression and television viewing would be shown to be spurious if, when controlling for the effect of the parents’ disciplining style, the relationship between television viewing and aggressive behavior were to go away.

Common-causal variables in correlational research designs can be thought of as “mystery” variables because, as they have not been measured, their presence and identity are usually unknown to the researcher. Since it is not possible to measure every variable that could cause both the predictor and outcome variables, the existence of an unknown common-causal variable is always a possibility. For this reason, we are left with the basic limitation of correlational research: Correlation does not demonstrate causation. It is important that when you read about correlational research projects, you keep in mind the possibility of spurious relationships, and be sure to interpret the findings appropriately. Although correlational research is sometimes reported as demonstrating causality without any mention being made of the possibility of reverse causation or common-causal variables, informed consumers of research, like you, are aware of these interpretational problems.

Stangor, C. (2017). Introduction to psychology. Boston, MA: Flatworld.

Correlational Research-Video

Summary

Correlational research designs have both strengths and limitations. One strength is that they can be used when experimental research is not possible because the predictor variables cannot be experimentally manipulated. Correlational designs also have the advantage of allowing the researcher to study behavior as it occurs in everyday life. We can also use correlational designs to make predictions—for instance, to predict the future success of employees who are in a training program from their scores on a set of ability tests. But if we want to answer questions about causality, such as to determine whether a particular job training program causes better job performance, then we must rely on experiments.

The defining feature of correlational research is that neither variable is manipulated. It does not matter how or where the variables are measured. A researcher could have participants come to a laboratory to complete a computerized backward digit span task and a computerized risky decision-making task and then assess the relationship between participants’ scores on the two tasks. Or a researcher could go to a shopping mall to ask people about their attitudes toward the environment and their shopping habits and then assess the relationship between these two variables. Both of these studies would be correlational because no independent variable is manipulated.

“Correlational Research.” Retrieved from http://open.lib.umn.edu/psychologyresearchmethods/chapter/7-2-correlational-research/. Licensed under CC-BY-NC-SA.